Théorème de Thébault

Le nom de théorème de Thébault ne correspond pas à un théorème précis, mais plutôt à une série de problèmes posés par le mathématicien français Victor Thébault (1882 - 1960).

Le problème de Thébault n^o 1

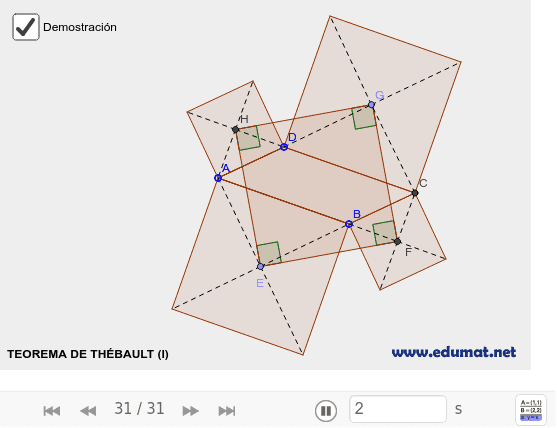
Le problème de Thébault n^o 1 est un problème de géométrie euclidienne portant sur le parallélogramme. Il fut posé par Thébault en 1937 qui le démontra en 1938^{[réf. nécessaire]}.

Ce théorème peut être considéré comme l'équivalent pour les quadrilatères du théorème de Napoléon qui concerne les triangles.

La rotation de centre O et d'angle ${\displaystyle {\frac {\pi }{2}}}$ transforme C en D, B en D', le carré de côté [CB] a pour image le carré de côté [DA].

Donc N a pour image P, soit ON = OP et l'angle ${\displaystyle {\widehat {NOP}}}$ est droit. NOP est un triangle rectangle isocèle en O.

De même par la rotation de centre M et d'angle ${\displaystyle {\frac {\pi }{2}}}$, le carré de côté [DA] a pour image le carré de côté [CB].

Donc P a pour image N ; MP = MN et le triangle NMP est rectangle isocèle en M.

MNOP a ses quatre angles droits et des côtés consécutifs égaux : c'est un carré.

Le problème de Thébault n^o 2

Le problème de Thébault n^o 2 est un problème de géométrie euclidienne portant sur le triangle équilatéral.

• Démonstration par raisonnement géométrique dans le cas externe

Par construction on a ${\displaystyle DC=DA}$ et ${\displaystyle CM=AL}$.

Comme ${\displaystyle {\widehat {DCM}}=90^{\circ } 60^{\circ }={\widehat {LAD}}}$ alors les triangles ${\displaystyle DCM}$ et ${\displaystyle DAL}$ sont superposables.

Ces deux triangles étant isocèles, on a pour les angles à-la-base ${\displaystyle {\widehat {CDM}}={\widehat {LDA}}={\frac {180^{\circ }-(90^{\circ } 60^{\circ })}{2}}=15^{\circ }}$.

Ainsi ${\displaystyle {\widehat {MDL}}=90^{\circ }-{\widehat {CDM}}-{\widehat {LDA}}=90^{\circ }-15^{\circ }-15^{\circ }=60^{\circ }}$.

Puisque ${\displaystyle {\widehat {MDL}}=60^{\circ }}$ et ${\displaystyle DM=DL}$, le triangle ${\displaystyle DML}$ est donc équilatéral.

• Démonstration par raisonnement géométrique dans le cas interne

Par construction on a ${\displaystyle AD=AL}$ et ${\displaystyle CD=CM}$.

Comme ${\displaystyle {\widehat {DAL}}=90^{\circ }-60^{\circ }={\widehat {MCD}}}$ alors les triangles ${\displaystyle DCM}$ et ${\displaystyle DAL}$ sont superposables.

Ces deux triangles étant isocèles, on a pour les angles à-la-base ${\displaystyle {\widehat {ADL}}={\widehat {MDC}}={\frac {180^{\circ }-(90^{\circ }-60^{\circ })}{2}}=75^{\circ }}$.

Ainsi ${\displaystyle {\widehat {MDL}}={\widehat {ADL}}-{\widehat {ADM}}}$

${\displaystyle ={\widehat {ADL}}-(90^{\circ }-{\widehat {MDC}})}$

${\displaystyle =75^{\circ }-(90^{\circ }-75^{\circ })}$

${\displaystyle =60^{\circ }}$

Puisque ${\displaystyle {\widehat {MDL}}=60^{\circ }}$ et ${\displaystyle DM=DL}$, le triangle ${\displaystyle DML}$ est donc équilatéral.

Le problème de Thébault n^o 3

Le problème de Thébault n^o 3, aussi connu sous le nom de Théorème de Sawayama-Thébault, est un théorème de géométrie euclidienne portant sur l'alignement de trois points

La première démonstration connue a été réalisée en 1973 par le mathématicien néerlandais H. Streefkerk.

Jean-Louis Ayme a publié, en 2003, une solution purement synthétique de ce problème. Il a également effectué des recherches historiques et a découvert que ce résultat avait été démontré en 1905 par Y. Sawayama, instructeur à l'école militaire de Tokyo.

Références

Voir aussi

Liens externes

• « Carré de Thébault - Théorème de Thébault », sur Descartes et les Mathématiques (une démonstration géométrique du théorème n^o 1)
• Michel Hort, « Le théorème de Thébault »

Article connexe

Théorème de van Aubel quand les carrés sont construits autour d'un quadrilatère quelconque

• Portail de la géométrie