Médiane de Tukey

En statistique, la médiane de Tukey est une statistique généralisant la médiane à des statistiques définies dans un espace de dimension supérieure à 1. Elle a été introduite par John Tukey en 1975. C'est un indicateur de tendance centrale.

Définition

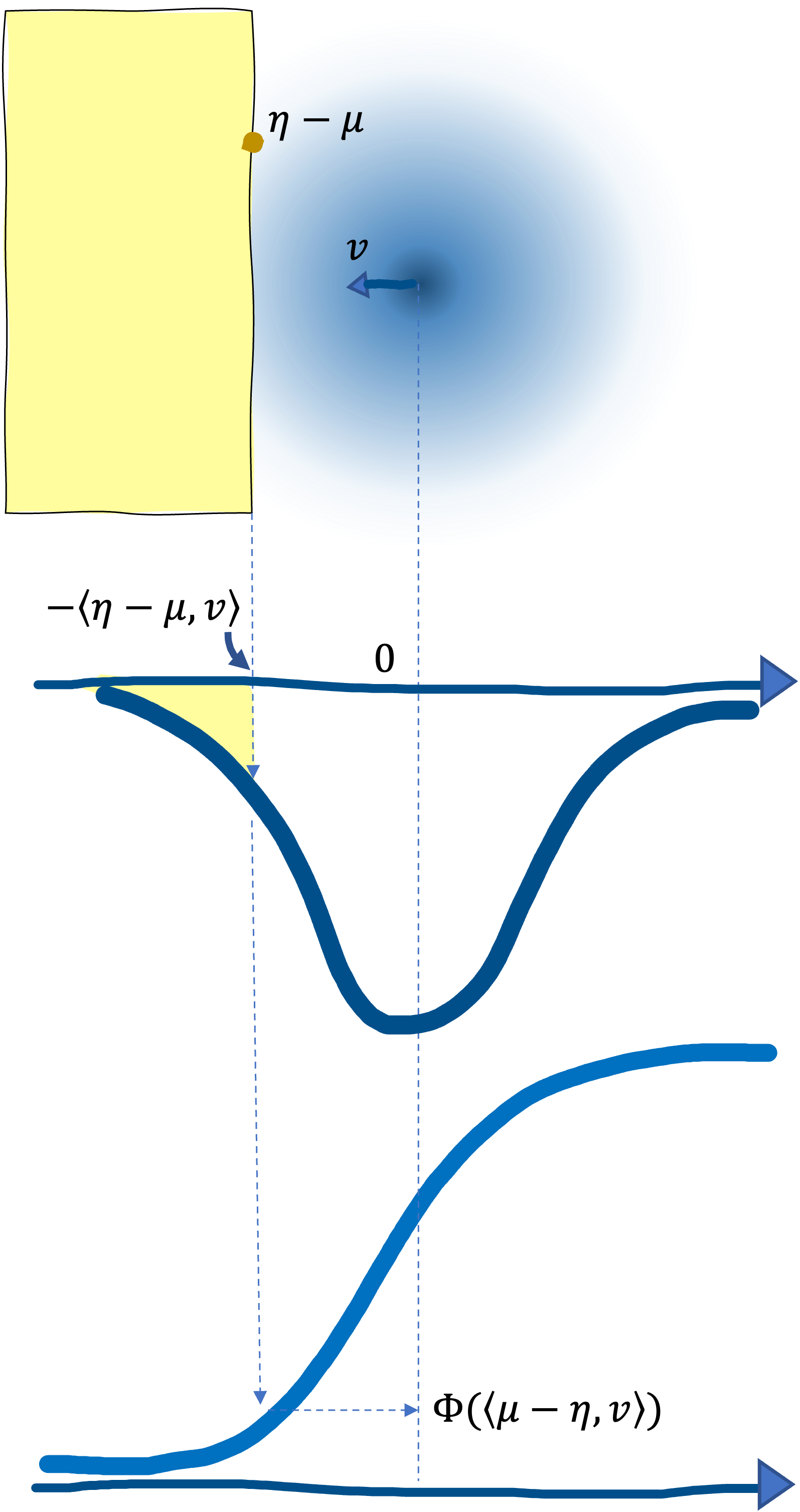
Soit X une variable aléatoire suivant une loi de probabilité ${\displaystyle \mathbb {P} }$ définie sur un espace de probabilités dans ${\displaystyle \mathbb {R} ^{n}}$. La profondeur de Tukey ou profondeur de demi-espace (halfspace depth) d'un point ${\displaystyle \mu \in \mathbb {R} ^{n}}$ est la probabilité minimale possible sur un côté d'un hyperplan passant par ${\displaystyle \mu \in \mathbb {R} ^{n}}$ :

${\displaystyle D_{\mathrm {Tukey} }(\mu ;\mathbb {P} )=\inf _{v\in \mathbb {R} ^{n}}\mathbb {P} (v^{T}(X-\mu )\geqslant 0).}$

La profondeur de Tukey peut être comprise comme la plus petite quantité d'observations qui peut être contenue dans un demi-espace dont la frontière passe par un point donné.

La médiane de Tukey d'une loi ${\displaystyle \mathbb {P} }$ est alors le points de profondeur de Tukey maximale :

${\displaystyle T(p)=\mathrm {arg} \max _{\mu \in \mathbb {R} ^{n}}D_{\mathrm {Tukey} }(\mu ;\mathbb {P} ).}$

Dans le cas où le problème de maximisation ci-dessus admet plusieurs solutions, on définira la médiane de Tukey comme le centre de gravité de l'ensemble solution.

Propriétés

En dimension 1, la médiane de Tukey est la médiane usuelle.

La médiane de Tukey est un indicateur de tendance centrale robuste.

Voir aussi

• Médiane géométrique
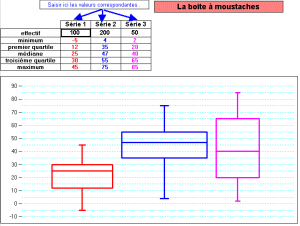
• Bagplot

Références

Bibliographie

• (en) Banghua Zhu, Jiantao Jiao et Jacob Steinhardt, « When does the Tukey median work? », .
• (en) Timothy M. Chan, An optimal randomized algorithm for maximum Tukey depth, Society for Industrial and Applied Mathematics, 2004, 430–436 p. (ISBN 978-0-89871-558-3, lire en ligne).

• Portail des probabilités et de la statistique